티스토리 뷰
접근법
소수 시리즈의 3탄이다. 소수가 싫어진다
소수 2탄과 유사한 문제의 형태이다. 범위가 주어지고, 해당 범위 안에서 소수를 찾는 문제다.
이번에는 전에 사용했던 함수들의 문제점을 조금 해결해보았다.
우선, for문의 반복 범위를 제곱근까지만 돌 수 있도록 변경했다.
반복의 횟수를 줄이는 것만으로 해도 충분히 시간을 줄일 수 있었고, 추가적으로 중간에 나누어 떨어지는 수가 있는
경우에는 즉시 False를 return하도록 했다. 그 코드는 바로 다음과 같다.
import math
def Prime(num):
if num==1:
return False
n=int(math.sqrt(num))
for i in range(2,n+1):
if num%i==0:
return False
return True
M, N = list(map(int,input().split(' ')))
for i in range(M,N+1):
if Prime(i) == True:
print(i)
그러나 내 생각에는 이 문제는 이렇게 하나씩 일일이 확인하는 것이 마찬가지로 비효율적이라는 생각이 들어서
새로운 방법을 고민해보다가, 주어진 입력값이 범위로 주어지므로 범위의 최댓값까지의 소수를 우선 먼저
구하는 것이 바람직할 것이라고 생각을 했다.
따라서, 최대 범위까지의 소수를 모두 구해 놓은 뒤에 최소 범위보다 큰 소수부터 차례로 출력될 수 있도록 했다.
그 방법으로 에라토스테네스의 체를 사용했다. 잠시 이해를 위해 위키백과의 자료를 첨부한다.
- 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
- 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
- 자기 자신을 제외한 2의 배수를 모두 지운다.
- 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
- 자기 자신을 제외한 3의 배수를 모두 지운다.
- 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
- 자기 자신을 제외한 5의 배수를 모두 지운다.
- 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
- 자기 자신을 제외한 7의 배수를 모두 지운다.
- 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
위 과정을 그림을 통해 살펴보면 이해하기 쉽다.
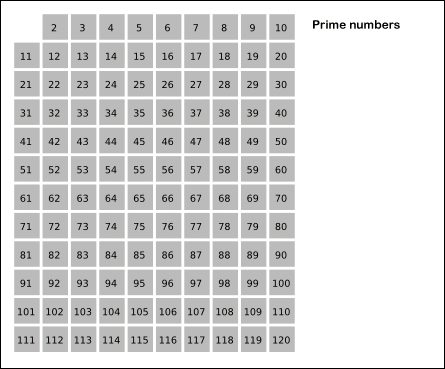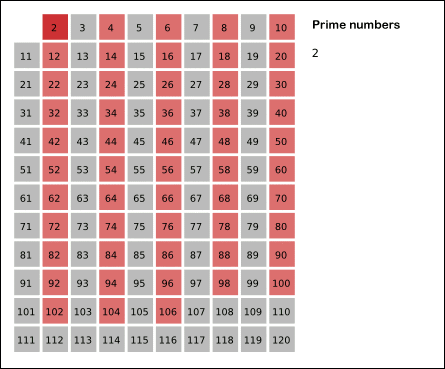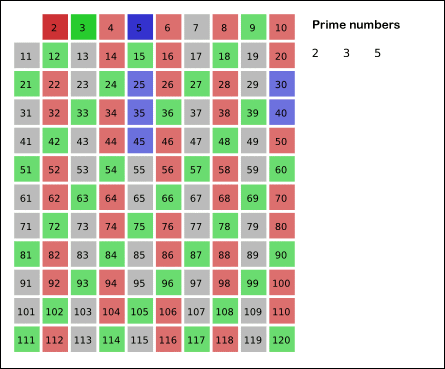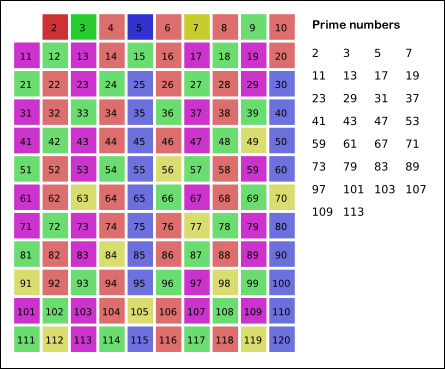
즉, 소수를 찾으면 소수의 배수는 모두 지워버리는 방법이다.
이 방법을 이용해서 주어진 범위의 소수를 조금 더 쉽게 구할 수 있었다.
우선 해당 범위까지의 숫자를 모두 순서대로 리스트에 채워 놓는다.
그다음 소수를 판별해서 소수일 경우에는 해당 값의 배수를 모두 0으로 바꿔주는 형태로 코드를 짜보았다.
여기서 0은 소수가 아닌 숫자를 의미하고, 이미 0으로 바뀌어버린 숫자의 경우는 소수가 아니므로
지나쳐가도록 continue를 사용했다.
풀이
M, N = list(map(int,input().split(' ')))
arr = [i for i in range(N+1)]
arr[1] = 0
for i in range(2,N+1):
if arr[i] == 0:
continue
for j in range(i*2,N+1,i):
arr[j] = 0
prime = [i for i in range(M,N+1) if arr[i] == i]
for i in prime:
if i >= M:
print(i)
'프로그래밍 > BOJ' 카테고리의 다른 글
| 백준 #9020: 골드바흐의 추측 (0) | 2020.01.26 |
|---|---|
| 백준 #4948: 베르트랑 공준 (0) | 2020.01.22 |
| 백준 #1978: 소수 (0) | 2020.01.22 |
| 백준 #1978: 소수 찾기 (0) | 2020.01.22 |
| 백준 #1011: Fly me to the Alpha Centauri (0) | 2020.01.19 |
